Odds Chance
Data Points
- There are a number of different terms used for probability in statistics.
- Each has a distinct (and usually precise) meaning.
- This article examines some of these terms and shows examples.
- Using the right terms can make your own data stories more understandable.



If you are confused about the difference between probability, chance, and odds, you're not alone. In their paper Confusion Between Odds and Probability, a Pandemic?[1] , Fulton et al. surveyed eight online dictionaries (including Cambridge, Macmillan, and Merriam-Webster), and found that while they all defined probability in a similar way, all eight gave 'inconsistent and computationally different definitions of the term odds.'
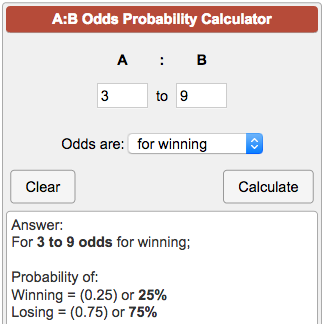
- The odds for the occurrence of an event are simply the probability of occurrence of an event, divided by the probability that the event does not occur. Or for example, if there are 8 equally likely individual outcomes, and 6 of them favor of an event, and 2 are against the event, then the odds for the occurrence of the event are '6 to 2', or '6.
- A 1 in 500 chance of winning, or probability of winning, is entered into this calculator as '1 to 500 Odds are for winning'. You may also see odds reported simply as chance of winning as 500:1. This most likely means '500 to 1 Odds are against winning' which is.
The question is, does it really matter if you use the correct definition? Or is it just enough to get your point across (as long as you do the math right)? It can be of vital importance to get the terminology right, especially if you're working in areas with significant monetary or social responsibilities. But in most cases, no one will be able to tell the difference and--unless you're publishing your work-- it's highly unlikely you'll be called out for making the wrong choice.
If you do work in a field where it's important to be precise, or you just want to clarify their definitions for your own purposes, here are short definitions of the three terms:
- Probability. The fraction you would expect to see a certain event occurring in many trials. It is expressed as a real number within the interval [0,1]. For example, the probability of event A happening might be 0.75. This is more formally known as the normalized probability.
- Chance or Likelihood. Chance, a synonym of probability, is usually expressed as a percentage (e.g. 75%). Chance is used primarily in weather predication, and typically indicates the likelihood of a given weather event occurring in a specific area over a certain period of time.
- Odds. Ratios of probabilities, they can be defined in two different ways: odds in favor of an event ('odds on') or against an event A ('Odds Against). Odds can be expressed as a ratio of the probability an event will happen divided by the probability an event won't happen: Odds in favor of A = A / (1 - A), usually simplified to lowest terms., For instance, if the probability of an event occurring is 0.75, then the odds for it happening are 0.75/0.25 = 3/1 = 3 to 1 for, while the probability that it doesn't occur is 1 to 3 against.
- American Gambling odds are often stated as plus or minus a number. For instance, on Oct 24, 2020, one betting house had the American Presidential race at Joe Biden at -185, Donald Trump at +135. These numbers generally reflect potential payouts - if you bet $100 on Biden, you'd only get a $50 payout (beyond your $100 invested) with implied odds of around 2 to 1 for, because Biden is the odds on favorite, while Trump would have a $135 payout with odds of 5 to 2 against.
- In statistics, there's also an odds ratio, which calculates the odds for two linked properties.The formula is slightly different, because it has to account for two events happening/not happening instead of one: OR = (a/c) / (b/d).
Odds, Probability, Chance: Example
Odds are derived from a probability as follows (Boston University): If the probability of an event is 0.8 (i.e. an 80% chance), then the odds are 0.8 / (1 - 0.8) = 0.8 / 0.2 = 4, or 4 to 1.
By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367 (since there are only 366 possible birthdays, including February 29). However, 99.9% probability is reached with just 70 people, and 50% probability with 23 people. Negative figures: The odds state how much must be bet to win £100 profit e.g. American odds of -120 would win £100 on a £120 bet. Implied Probability Odds correlate to probability e.g a 3/1 bet is expected to win one in every 4 attempts, hence the probability is 25%.
The following picture clarifies the difference between probability and odds, using an American roulette wheel with 18 black spaces, 18 red spaces, and 2 green (0 and 00 pockets):
Summary
While these aren't comprehensive, probability can be expressed in various ways, and knowing the distinctions between these ways can lend you more credibility when talking with stakeholders or audiences. This is also critical when gathering this type of information, as consistency in usage makes analyzing trends possible in the first place.
References
Roulette Wheel image: Ralf Roletschek, CC BY-SA 3.0 a href='https://creativecommons.org/licenses/by-sa/3.0%3E'>https://creativecommons.org/licenses/by-sa/3.0>;, via Wikimedia Commons
Problem: A spinner has 4 equal sectors colored yellow, blue, green and red. What are the chances of landing on blue after spinning the spinner? What are the chances of landing on red?
Solution: The chances of landing on blue are 1 in 4, or one fourth.
The chances of landing on red are 1 in 4, or one fourth.
This problem asked us to find some probabilities involving a spinner. Let's look at some definitions and examples from the problem above.
| Definition | Example |
| An experiment is a situation involving chance or probability that leads to results called outcomes. | In the problem above, the experiment is spinning the spinner. |
| An outcome is the result of a single trial of an experiment. | The possible outcomes are landing on yellow, blue, green or red. |
| An event is one or more outcomes of an experiment. | One event of this experiment is landing on blue. |
| Probability is the measure of how likely an event is. | The probability of landing on blue is one fourth. |
In order to measure probabilities, mathematicians have devised the following formula for finding the probability of an event.
| Probability Of An Event | |||
|
The probability of event A is the number of ways event A can occur divided by the total number of possible outcomes. Let's take a look at a slight modification of the problem from the top of the page.
Experiment 1: A spinner has 4 equal sectors colored yellow, blue, green and red. After spinning the spinner, what is the probability of landing on each color?
The possible outcomes of this experiment are yellow, blue, green, and red.
Probabilities:
| P(yellow) | = | # of ways to land on yellow | = | 1 |
| total # of colors | 4 | |||
| P(blue) | = | # of ways to land on blue | = | 1 |
| total # of colors | 4 | |||
| P(green) | = | # of ways to land on green | = | 1 |
| total # of colors | 4 | |||
| P(red) | = | # of ways to land on red | = | 1 |
| total # of colors | 4 |
Experiment 2: A single 6-sided die is rolled. What is the probability of each outcome? What is the probability of rolling an even number? of rolling an odd number?
Outcomes: The possible outcomes of this experiment are 1, 2, 3, 4, 5 and 6.
Probabilities:
| P(1) | = | # of ways to roll a 1 | = | 1 | ||
| total # of sides | 6 | |||||
| P(2) | = | # of ways to roll a 2 | = | 1 | ||
| total # of sides | 6 | |||||
| P(3) | = | # of ways to roll a 3 | = | 1 | ||
| total # of sides | 6 | |||||
| P(4) | = | # of ways to roll a 4 | = | 1 | ||
| total # of sides | 6 | |||||
| P(5) | = | # of ways to roll a 5 | = | 1 | ||
| total # of sides | 6 | |||||
| P(6) | = | # of ways to roll a 6 | = | 1 | ||
| total # of sides | 6 | |||||
| P(even) | = | # ways to roll an even number | = | 3 | = | 1 |
| total # of sides | 6 | 2 | ||||
| P(odd) | = | # ways to roll an odd number | = | 3 | = | 1 |
| total # of sides | 6 | 2 |
Experiment 2 illustrates the difference between an outcome and an event. A single outcome of this experiment is rolling a 1, or rolling a 2, or rolling a 3, etc. Rolling an even number (2, 4 or 6) is an event, and rolling an odd number (1, 3 or 5) is also an event.
In Experiment 1 the probability of each outcome is always the same. The probability of landing on each color of the spinner is always one fourth. In Experiment 2, the probability of rolling each number on the die is always one sixth. In both of these experiments, the outcomes are equally likely to occur. Let's look at an experiment in which the outcomes are not equally likely.
Experiment 3: A glass jar contains 6 red, 5 green, 8 blue and 3 yellow marbles. If a single marble is chosen at random from the jar, what is the probability of choosing a red marble? a green marble? a blue marble? a yellow marble?
Outcomes: The possible outcomes of this experiment are red, green, blue and yellow.
Probabilities:
| P(red) | = | # of ways to choose red | = | 6 | = | 3 |
| total # of marbles | 22 | 11 | ||||
| P(green) | = | # of ways to choose green | = | 5 | ||
| total # of marbles | 22 | |||||
| P(blue) | = | # of ways to choose blue | = | 8 | = | 4 |
| total # of marbles | 22 | 11 | ||||
| P(yellow) | = | # of ways to choose yellow | = | 3 | ||
| total # of marbles | 22 |
The outcomes in this experiment are not equally likely to occur. You are more likely to choose a blue marble than any other color. You are least likely to choose a yellow marble.
Experiment 4: Choose a number at random from 1 to 5. What is the probability of each outcome? What is the probability that the number chosen is even? What is the probability that the number chosen is odd?
Outcomes: The possible outcomes of this experiment are 1, 2, 3, 4 and 5.
Probabilities:
How To Find The Odds Of Something
| P(1) | = | # of ways to choose a 1 | = | 1 |
| total # of numbers | 5 | |||
| P(2) | = | # of ways to choose a 2 | = | 1 |
| total # of numbers | 5 | |||
| P(3) | = | # of ways to choose a 3 | = | 1 |
| total # of numbers | 5 | |||
| P(4) | = | # of ways to choose a 4 | = | 1 |
| total # of numbers | 5 | |||
| P(5) | = | # of ways to choose a 5 | = | 1 |
| total # of numbers | 5 | |||
| P(even) | = | # of ways to choose an even number | = | 2 |
| total # of numbers | 5 | |||
| P(odd) | = | # of ways to choose an odd number | = | 3 |
| total # of numbers | 5 |
The outcomes 1, 2, 3, 4 and 5 are equally likely to occur as a result of this experiment. However, the events even and odd are not equally likely to occur, since there are 3 odd numbers and only 2 even numbers from 1 to 5.
Summary: The probability of an event is the measure of the chance that the event will occur as a result of an experiment. The probability of an event A is the number of ways event A can occur divided by the total number of possible outcomes. The probability of an event A, symbolized by P(A), is a number between 0 and 1, inclusive, that measures the likelihood of an event in the following way:
- If P(A) > P(B) then event A is more likely to occur than event B.
- If P(A) = P(B) then events A and B are equally likely to occur.
Exercises
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.
| 1. | Which of the following is an experiment? |
Odds Of Life Happening By Chance
| 2. | Which of the following is an outcome? |
| 3. | Which of the following experiments does NOT have equally likely outcomes? |
Odds Vs Chances
| 4. | What is the probability of choosing a vowel from the alphabet? |
Odds And Chance
| 5. | A number from 1 to 11 is chosen at random. What is the probability of choosing an odd number? |